¿Cuántas especies hay? Una actualización para las primeras dos décadas del siglo XXI

Por:   Jorge Mercado, Tania Escalante Espinosa

En 2003 (hace 20 años ya), uno de los presentes autores publicó un manuscrito en esta revista sobre cuántas especies hay, que ha sido muy usado en diversas partes del mundo hispanohablante, con más de 100 citas y leído más de 20,000 veces, según el portal ResearchGate (2022). Sin embargo, la pregunta sobre cuál es el número de especies que habita el planeta sigue vigente. Parte del problema es que no podemos simplemente contar el número de formas de vida, ya que muchos seres vivos se encuentran en hábitats inaccesibles, otros son demasiado pequeños para verlos a simple vista (algunos hasta con potentes microscopios son difíciles de identificar), unos más no son fácilmente detectables o, incluso, algunos habitan dentro de otros seres vivos.

     Un problema al considerar las formas de vida es, por ejemplo, decidir sobre si un virus es una especie o si los individuos producto de hibridación son especies y, por lo tanto, esto también dificulta conocer realmente el número de especies. De hecho, el problema es tan profundo que en la actualidad no se ha llegado a un consenso en la definición de qué es una especie.

     Existen diferentes compendios que han intentado definir la especie, lo que ha llevado a proponer conceptos como el biológico, el evolutivo, el filogenético, entre otros; pero sin llegar a un acuerdo sobre cuál es el más adecuado.

     Con el fin de poder realizar estimaciones más reales del número de especies, diferentes científicos han llevado a cabo inventarios de fauna y flora, visitando áreas inexploradas, inventariando grupos poco conocidos, registrando nuevas especies o empleando modelos matemáticos que permitan aproximarse hacia cuál es el número de especies que existe en el planeta. Dentro de estas estimaciones o modelos matemáticos, uno de los acercamientos más empleados el día de hoy es el de Mora et al. (2011), quienes estimaron alrededor de los 8.7 millones de especies en la superficie terrestre y los océanos. No obstante, el número exacto de especies aún es desconocido y podría estar lejos de ser calculado realmente algún día, dada la destrucción de los hábitats, lo inaccesible de ciertos lugares, y la falta de exploración hacia grupos taxonómicos como microalgas, dinoflagelados, bacterias, hongos y virus.

     Pero, finalmente, ¿cómo medimos el número de especies? Una de las herramientas más empleadas es el uso de índices que permiten medir la relación entre el número de individuos y especies por una unidad de área determinada. En 1960, el ecólogo vegetal Robert H. Whittaker, mediante el análisis de la vegetación a través de un gradiente altitudinal en las montañas Siskiyou (en Oregon y California, Estados Unidos), consideró necesario organizar la diversidad de forma jerárquica.

     Whittaker (1960) propuso que la riqueza de especies de una comunidad es la diversidad alfa (α), el grado de diferenciación entre comunidades es la diversidad beta (β), y la diversidad resultante de todas las comunidades es la diversidad gamma (γ). La anterior estructura jerárquica de la diversidad permite establecer la estructura de las comunidades (Figura 1).

     ¿Pero, por qué no solo contar el número de especies y así saber cuántas existen? La respuesta es que el número real está sesgado por el esfuerzo de muestreo: los valores de riqueza cambian dependiendo de cuánto tiempo se invierte en la recolecta científica, del tipo de muestreo que se emplea y el periodo del año, entre otros factores. Por ejemplo, en los bosques que son secos estacionalmente, es muy probable que la diversidad de insectos cambie ligeramente durante los periodos de lluvia y sequía. Por lo anterior, se requiere de metodologías que permitan hacer estimaciones de la riqueza considerando estos factores. Whittaker (1960) mencionó también que la diversidad alfa podría analizarse teniendo en cuenta las abundancias de las especies; es decir, el número de individuos de una especie en un área dada.

     La abundancia permite identificar a las especies raras, las cuales son aquellas que presentan uno o dos registros por localidad, y a las comunes, que presentan más de dos registros por localidad (Colwell y Coddington, 1994). Para Chao et al. (2014), la abundancia influye en la diversidad: si tenemos dos localidades y contamos todas las especies por igual, sin tomar en cuenta su abundancia, simplemente las especies raras “valdrán” lo mismo que las comunes. Pero, ¿qué pasa cuando tenemos dos localidades donde la riqueza de especies es idéntica, pero las especies raras en una localidad son las comunes en la segunda y viceversa?, ¿la diversidad es realmente la misma? De hecho, sería clave incorporar datos de abundancia para poder realizar estimaciones realistas de la diversidad y no solo realizar los análisis con base en los datos de presencia-ausencia de las especies.

ÍNDICES DE DIVERSIDAD ALFA

En términos generales, los índices de diversidad alfa se pueden dividir en dos grupos: los que evalúan la riqueza de especies (cuántos tipos hay) y los que calculan la uniformidad o dominancia de las especies (cómo se distribuyen los individuos entre las especies).

     En el primer grupo se incluyen aquellos índices que solo tienen en cuenta la lista de especies, es decir, su composición; mientras que en el segundo se consideran los valores de abundancia de cada individuo y su relación con el área. El primer grupo incluye índices que permiten medir la riqueza como el de Margalef, las curvas de acumulación, las curvas de rarefacción y de interpolación-extrapolación. Estas últimas son sumamente útiles, ya que han permitido calcular el número esperado de especies de cada muestra al estandarizarlas a un mismo tamaño. Por su parte, el índice de Margalef compensa los efectos del tamaño de la muestra, dividiendo el número de especies en una muestra por el logaritmo natural del número de organismos recolectados, y así tratar de evitar el problema de los sesgos de los muestreos.

     En el segundo grupo de índices, o aquellos que requieren las abundancias de las especies, se han empleado de forma tradicional diferentes estimadores, los cuales incluyen a los índices de Shannon-Weaver y Simpson (Guiasu, 2012). El índice de Shannon-Weaver asume que los individuos se muestrean aleatoriamente de una gran población independiente y que todas las especies están representadas en la muestra. Este índice se calcula tomando en cuenta la proporción del número total de individuos de cada especie: cuanto mayor sea el índice, mayor será la diversidad de especies. Lo anterior permite medir la diversidad con “uniformidad”, lo que refiere a la proporción en la cual cada especie forma parte del todo (Jost y González-Oreja, 2012). Por otro lado, el índice de Simpson toma en cuenta el número de especies presentes, pero también su abundancia relativa: a medida que aumenta la riqueza y la uniformidad de las especies, también aumenta la diversidad.

     Los índices anteriores han sido de gran utilidad para comprender cómo se estructura una comunidad en su diversidad alfa; sin embargo, un problema de estas medidas es que sus resultados no permiten realmente una comparación directa entre las localidades porque no miden la diversidad de manera directa, sino la “entropía”. La entropía se refiere a la incertidumbre que existe sobre si un individuo seleccionado al azar de la comunidad pertenece a cierta especie, por lo que, si tenemos una comunidad donde todas las especies poseen la misma abundancia, entonces la entropía será alta y tendrá mayor diversidad (Jost, 2006; Moreno et al., 2011).

DIVERSIDAD VERDADERA Y NÚMEROS EFECTIVOS

Jost (2006) empleó el concepto de diversidad “verdadera” basada en los números de Hill (1973), para identificar formas de evaluar la diversidad de especies de manera consistente. Esta medida de la diversidad “verdadera” son los números efectivos de especies, a los cuales corresponde el número de elementos igualmente probables, necesarios para producir el valor dado del índice de diversidad (Jost, 2007). Jost mostró que la diversidad en ecología no corresponde al valor del índice de diversidad en sí mismo, sino a los números equivalentes o efectivos. Aunque el concepto “verdadero” puede ser cuestionable, el autor se refiere a este para diferenciarlo de otras medidas o índices que no cumplen con las propiedades intuitivas de la diversidad (Moreno et al., 2011).

     Los números efectivos de especies tienen al menos dos propiedades vinculadas estrechamente con la diversidad alfa, lo que facilita su uso en otro tipo de análisis como los filogenéticos y los funcionales (Jost, 2006, 2007; Chao et al., 2014; Cao y Hawkins, 2019): 1) permiten que la diversidad alfa y beta varíe independientemente entre sí a través de regiones con diferentes diversidades gamma; y 2) su valor se expresa en las mismas cantidades y unidades, por lo que es posible visualizar las diferencias en la diversidad, de modo que los componentes dentro de la comunidad y entre comunidades se pueden comparar directamente. Otra ventaja de los números efectivos es que dependen menos del esfuerzo de muestreo que de la riqueza de especies (Beck y Schwanghart, 2010; Chao et al., 2014), por lo que proporcionan evaluaciones de biodiversidad mejor interpretables y comparables.

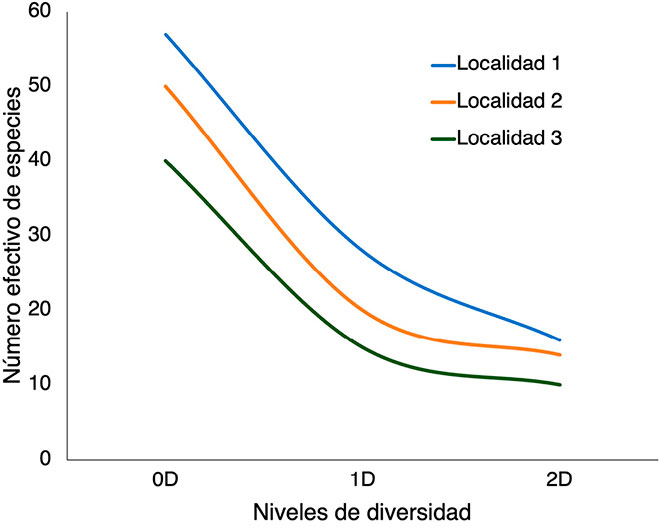
     Dentro de la propuesta abordada por Jost (2006) sobre los índices de diversidad verdadera –que también se nombran como “números de Hill”–, el número efectivo de especies se divide en tres niveles (Jost, 2006; Chao et al., 2014b; Marcon y Hérault, 2015; Figura 2): 1) la diversidad del orden cero (⁰D) o riqueza de especies; 2) la diversidad del orden uno (¹D) o exponencial del índice de Shannon, que pondera la diversidad por la abundancia relativa de las especies; y 3) la diversidad del orden dos (²D), o inverso del índice de Simpson, que toma en cuenta las especies más abundantes.

CÓMO SE APLICAN LOS NÚMEROS EFECTIVOS DE ESPECIES

Para ejemplificar el uso de los números efectivos, presentaremos el caso de tres localidades en las que se realizó recolecta de insectos con el fin de identificar cómo la perturbación humana (por ejemplo, la implementación de cultivos y sistemas de pastoreo para ganado) ha afectado la diversidad en los bosques secos tropicales. En nuestro ejemplo, usaremos la Figura 2, donde la primera localidad corresponde a un bosque nativo, la segunda al borde del bosque y la localidad 3 a un área con perturbación antrópica.

En el bosque nativo se obtuvieron los siguientes valores de diversidad: ⁰D=57, ¹D=28 y ²D=16. Para el borde del bosque: ⁰D=50, ¹D=20, ²D=14. Finalmente, para el área perturbada: ⁰D=40, ¹D=15 y ²D=10.

     Es importante notar que, a diferencia de los índices tradicionales, acá es posible hacer una comparación entre las localidades en términos numéricos, los cuales pueden ser interpretados de una forma más sencilla; por ejemplo, el bosque presenta siete especies más que el borde del bosque y 17 más que las áreas perturbadas, en términos de riqueza. Igualmente, el bosque presenta 8 especies efectivas más que el borde del bosque y 13 que las áreas perturbadas (diversidad de Shannon). Finalmente, el bosque presenta dos especies efectivas dominantes más que el borde del bosque y seis más que las áreas perturbadas (diversidad de Simpson).

     En general, se observa una tendencia hacia la disminución del número de especies (⁰D) conforme se avanza desde el bosque nativo hacia el área perturbada. Respecto al número de especies efectivas (¹D), el bosque nativo tiene más diversidad que las otras dos localidades, y lo mismo ocurre con el número de especies dominantes (²D). Esto sugiere que, en general, la perturbación antrópica es un fenómeno que tiene un sustancial efecto negativo en la diversidad.

     De esta forma, los números efectivos de especies pueden brindar información más precisa de cómo el impacto antrópico afecta la diversidad de los ecosistemas, tanto a nivel de riqueza, homogeneidad y dominancia.

     Aunque nuestro ejemplo es muy simple, para el cálculo de los números de Hill existen diferentes paquetes producidos en el ambiente del software estadístico R (por ejemplo: iNEX, Entropart, entre otros), que permiten su cálculo de forma más eficiente y fácil.

     Además, estos paquetes permiten calcular intervalos de confianza, para explorar si existen diferencias significativas entre las comunidades analizadas, en los tres niveles de los números efectivos de especies.

     Los números efectivos pueden ser empleados para proponer áreas prioritarias para la conservación de la biodiversidad, más aún cuando los extendemos hacia otras dimensiones de la diversidad biológica, como la filogenética o la funcional. Así, estas medidas nos permitirán tener más información para intentar conocer el número de especies que existe en el planeta.

REFERENCIAS

Beck J and Schwanghart W (2010). Comparing measures of species diversity from incomplete inventories: an update. Methods in Ecology and Evolution 1:38-44.

Cao Y and Hawkins CP (2019). Weighting effective number of species measures by abundance weakens detection of diversity responses. Journal of Applied Ecology 56:1200-1209.

Chao A, Gotelli N, Hsieh TC, Sander E, Ma KH, Colwell RK and Ellison AM (2014). Rarefaction and extrapolation with Hill numbers: a framework for sampling and estimation in species diversity studies. Ecological Monographs 84:1557-7015.

Colwell RK and Coddington JA (1994). Estimating Terrestrial Biodiversity through Extrapolation. Philosophical Transactions: Biological Sciences 345:101-118.

Guiasu RC and Guiasu S (2012). The Weighted Gini-Simpson Index: Revitalizing an Old Index of Biodiversity. International Journal of Ecology 478728.

Hill M (1973). Diversity and evenness: a unifying notation and its consequences.  Ecology 54:427-432.

Jost L (2006). Entropy and Diversity. Okios 113:363-374.

Jost L (2007). Partitioning diversity into independent alpha and beta components. Ecology 88:2427-2439.

Jost L y González-Oreja J (2012). Midiendo la diversidad biológica: más allá del índice de Shannon. Acta zoológica lilloana 56:3-14.

Marcon E and Hérault B (2015). entropart: An R Package to Measure and Partition Diversity. 67:26.

Mora C, Tittensor DP, Adl S, Simpson AGB and Worm B (2011). How Many Species Are There on Earth and in the Ocean? PLOS Biology 9:e1001127.

Moreno C, Barragán F, Pineda E y Pavón P (2011). Reanalizando la diversidad alfa: alternativas para interpretar y comparar información sobre comunidades ecológicas. Revista Mexicana de Biodiversidad 82:1249-1261.

Researchgate (2022) Recuperado de: https://www.researchgate.net.

Whittaker R (1960). Vegetation of the Siskiyou mountains, Oregon and California. Ecological Monographs 30:279-338.